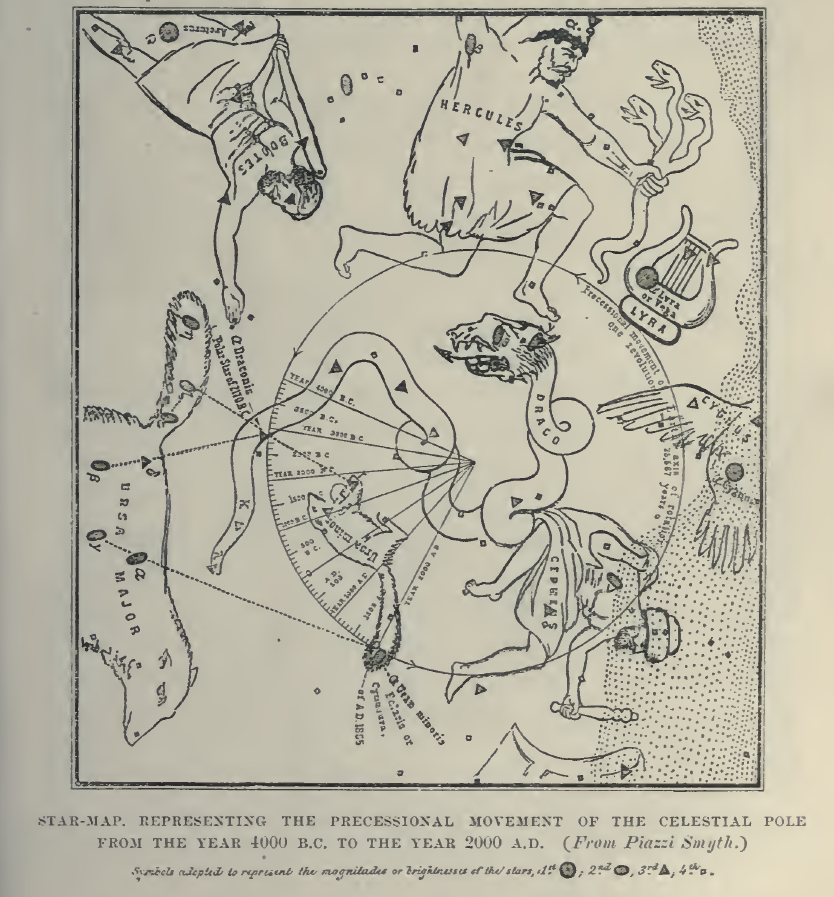
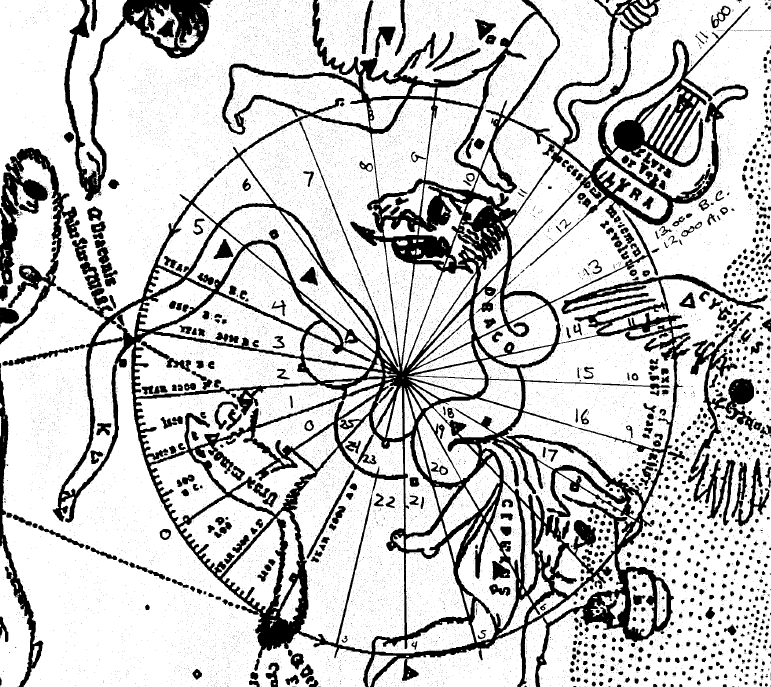
Piazzi Smyth

We are in search of VEGA remember. Reader, continue the scale back, from 4000 B.C. to 12,098 B.C. - 13,465 B.C. I guess ~11,600 B.C. for Vega to "center" itself. Close enough to be the Pole Star of the Ancients.

So, the ~13,000 B.C. build date of the Great Pyramid, is accurate. Nice work Edward, nice work. The LORD has directed the Hiddekelic's to build the altar just prior to their destruction - part of the grand plan of redemption. The Pole Star was moving from Cygnus to Vega.

29,789 B.C., the first creation of man, the pole star was Alpha Draconis,

(and was again about 2170 B.C., which matches markings on this original chart, and in the main entrance tunnel of the pyramid.)

23,017 B.C., the second creation of man, the pole star was Polaris. 13,465 B.C., the third creation of man, the pole star was half way between Cygnus and Vega. 3,897 B.C., the fourth creation of man, the pole star was approaching Alpha Draconis again.

The wheel keeps rotating until we reach Alpha Draconis, have we come full circle? ...with only a thin slice of "time" left to what end?

33,560 years ago, the pole star is pointing straight up on this chart, but to what? Time to get the star charts out.

If you notice, looking back at 3853 A.D. the final demise of aggregate matter, it lines up with 21,414 B.C. or close at 3586 A.D. the Euphratic 1st Age "the white race destruction", with only a 267 year variance.

Take notice please to the Dates.

. . . .

A Word from J. Norman Lockyer 1894

"In the last chapter I referred to one of the difficulties (See Chap. xii. "Dawn of Astronomy" Lockyer 1894.) of modern inquiries into the orientation of ancient temples, which arises from the fact that the sun has not always, at the solstices, risen or set at exactly the same points of the horizon. We now find ourselves face to face with the fact that the stars do not rise or set at the same points century after century. We saw that the change in the position of the sun on the horizon at the solstices is due to a very small change of obliquity of the ecliptic, so that in a matter of something like 6,000 years the position of the sun at sunrise and sunset on the horizon may be varied by, roughly speaking, 1 degree. But in the case of the stars the matter is very much more serious, because in the course of something like 13,000 years the - rising or setting - places of a star may vary by something like 47° along the horizon north or south.

So that in the cases both of sun and stars there is no real fixity in the places of rising or setting, although of course those who made the first observations and built the first temples were not in a position to know this.

The real cause of this precessional movement which causes the stars to change their places lies in the fact that the earth is not a sphere, its equatorial diameter being longer than its polar diameter, so that there is a mass of matter round the equator in excess of what we should get if the earth were spherical. Suppose that matter to be represented by a ring. The ring is differently presented to the sun, one part being nearer than the other, the nearer part being attracted more forcibly. If we take the point in the ring nearest the sun where there is the greatest attraction, and draw a line to the opposite point where the attraction is least, we can show that the case stands in this way: the sun's pull may be analysed into two forces, one of them represented by the line joining the centre of the sun and the centre of the ring, and another at right angles to it let fall from the point most strongly attracted on to the first line. The question is, what will that force at right angles do?

The figure below represents a model illustrating the rotation of the earth on its axis, and the concurrent revolution of the sun round the earth once a year. To represent the downward force it is perfectly fair if I add a weight. The moment this is done the axis of the gyroscope representing the earth's axis, instead of retaining its direction to the same point as it did before, now describes a circle round the pole of the heavens.

It is now a recognised principle that there is, so to speak, a wobble of the earth's axis round the pole of the heavens, in consequence of the attraction of the sun on the nearer point of this equatorial ring being greater than on the part of the ring further removed from it. That processional movement is not quite so simple as it is shown by the model, because what the sun does in this way is done to a very much larger extent by the moon, the moon being so very much nearer to us.

In consequence, then, of this luni-solar precession we have a variation of the points of intersection of the planes of the earth's equator and of the ecliptic; in consequence of that we have a difference in the constellations in which the sun is at the time of the solstices and the equinoxes; and, still more important from our present point of view, we have nother difference, viz., that the declinations, and therefore the amplitudes, and therefore the places of setting and rising of the stars, change from century to century.

Now that we have thus become acquainted with the physical cause of that movement of the earth's axis which gives rise to what is called the precession of the equinoxes, we have next to enter with somewhat greater detail into some of the results of the movement.

The change of direction of the axis in space has a cycle of something between 25,000 and 26,000 years. As it is a question of the change of the position of the celestial equator, or rather of the pole of the celestial equator, amongst the stars in relation to the pole of the heavens, of course the declinations of stars will be changed to a very considerable extent; indeed, we have seen that the declination of a star can vary by twice the amount of the obliquity, or say 47°, so that a star at one time may have zero declination — that is, it may lie on the equator — and at another it may have a declination 47° N. or S. Or, again, a star may be the pole star at one particular time, and at another it will be distant from the pole no less than 47°. Although we get this enormous change in one equatorial co-ordinate, there would from this cause alone be practically no change with regard to the corresponding ecliptic co-ordinate — that is to say, the position of the star with reference to the earth's movement round the sun. This movement takes place quite independently of the direction of the axis, so that while we get this tremendous swirl in declination, the latitudes of the stars or their distances from the ecliptic north or south will scarcely change at all.

Among other important results of these movements dependent upon precession we have the various changes in the polestar from period to period, due to the various positions occupied by the pole of the earth's equator. We thus see how in this period of 25,000 years or thereabouts the pole-stars will change, for a pole-star is merely the star near the pole of the equator for the time being. At present, as we all know, the pole-star is in the constellation Ursa Minor. During the last' 25,000 years the pole-stars have been those lying nearest to a curved line struck from the pole of the heavens with a radius equal to the obliquity of the ecliptic, which, as we have seen, is liable to change within small limits; so that about 10,000 or 12,000 years ago the pole-star was no longer the little star in Ursa Minor that we all know, but the bright star Vega, in the constellation Lyra. Of course 25,000 years ago the pole-star was practically the same as it is at present. Associated with this change in the pole-star, the point of intersection of the two fundamental planes (the plane of the earth's rotation and the plane of the earth's revolution) will be liable to change, and the period will be the same—about 25,000 years. Where these two planes cut each other we have the equinoxes, because the intersection of the planes defines for us the vernal and the autumnal equinoxes; when the sun is highest and lowest half-way between these points we have the solstices. In a period of 25,000 years the star which is nearest to an equinox will return to it, and that which is nearest a solstice will return to it. During the period there will be a constant change of stars marking the equinoxes and the solstices.

The chief points in the sun's yearly path then will change among the stars in consequence of this precession. It is perfectly clear that if we have a means of calculating back the old positions of stars, and if we have any very old observations, we can help matters very much, because the old observations if they were accurately made would tell us that such and such a star rose with the sun at the solstice or at the equinox at some special point of ancient time. If it be possible to calculate the time at which the star occupied that position with regard to the sun, we have an astronomical means of determining the time, within a few years, at which that particular observation was made.

Fortunately, we have such a means of calculation, and it has been employed very extensively at different periods, chiefly bv M. Biot in France, and quite recently by German astronomers, in calculating the positions of the stars from the present time to a period of 2000 years B.C. We can thus determine with a very high degree of accuracy the latitude, longitude, right ascension, declination, and the relation of the stars to an equinox, a solstice, or a pole, as far back as we choose. Since we have the planes of the equator and ecliptic cutting each other at different points in consequence of the cause which I have pointed out — the attraction of the sun and moon — we have a fixed equator and a variable equator depending upon that. In consequence of the attraction of the planets upon the earth, the plane of the ecliptic itself is not fixed, so that we have not only a variable equator, but also a variable ecliptic. What has been done in these calculations is to determine the relations and the results of these variations.

The calculations undertaken for the special purposes of this book will be referred to later.

A simpler, though not so accurate a method consists in the use of a precessional globe. In this we have two fixed points at the part of the globe representing the poles of the heavens, on which the globe may be rotated; when this is done the stars move absolutely without any reference to the earth or to the plane of the equator, but purely with reference to the ecliptic. We have, then, this globe quite independent of the earth's axis. How can we make it dependent upon the earth's axis We have two brass circles at a distance of 23° from each pole of the heavens (north and south); these represent the circle described by the pole of the earth in the period of 25,000 years. In these circles are forty-eight holes in which I can fix two additional clamping screws, and rotate the globe with respect to them by throwing out of gear the two points which produced the ecliptic revolution.

If I use that part of the brass circle which is occupied by our present pole-star, we get the apparent revolution of the heavens with the earth's axis pointing to the pole-star of today. If we wish to investigate the position of things, say 8,000 years ago, we bring the globe back again to its bearings, and then adjust the screws into the holes in the brass circles which are proper for that period. When we have the globe arranged to 6000 years B.C. (i.e., 8,000 years ago), in order to determine the equator at that time all we have to do is to paint a line on the globe in some water-colour, by. holding a camel's-hair pencil at the east or west point of the wooden horizon. That line represents the equator 8,000 years ago. Having that line, of course, the intersection of the equator with the ecliptic will give us the equinoxes, so that Ave may affix a wafer to represent the vernal equinox. Or if we take that part of the ecliptic which is nearest to the North Pole, and, therefore, the N. declination of which is greatest, viz., 23-1/2° N., we have there the position of the sun at the summer solstice, and 23-1/2° S. will give us the position of the sun at the winter solstice. So by means of such a globe as this it is possible to determine roughly the position of the equator among the stars, and note those four important points in the solar year, the two equinoxes and the two solstices. I have taken a period of 8,000 years, but I might just as easily have taken a greater or a smaller one. By means of this arrangement, therefore, we can determine within a very small degree of error, without any laborious calculations, the distance of a star north or south of the equator, i.e., its declination, at any point of past or future time.

The positions thus found, say, for intervals of 500 years, may be plotted on a curve, so that we can, with a considerable amount of accuracy, obtain the star's place for any year. Thus the globe may be made to tell us that in the year 1000 A.D. the declination of Fomalhaut was 35° S., in 1000 B.C. it was 42°, in 2000 it was about 44°, in 4000 it was a little over 42° again, but in 6000 b.c. it had got up to about 33°, and in 8000 B.C. to about 22°.

The curve of Capella falls from 41° N. at 0 A.D. to 10° at 5500 B.C., so we have in these 5500 vears in the case of this star run through a large part of that variation to which I have drawn attention.

I have ascertained that the globe is a very good guide indeed within something of like 1° of declination. Considering the difficulty of the determination of amplitudes in the case of buildings, it is clear that the globe may be utilised with advantage, at all events to obtain a first approximation." 

. . . .

And, an Astronomy Lesson from Worthy:
Precession of Earth.

"The phenomenon we call "precession" was discovered by Greek astronomer Hipparchus when he compared his own circa 200 BC records with older charts. What he saw was that the equinoxes in his day (where the sun's path crosses the celestial equator) were in a different position among the stars than the 150-year-old comparison charts showed. This is due to a gyroscopic wobble of earth's spin axis that takes 26000 years to complete. In this wobble motion, the tilt of the earth stays roughly constant at 23.4 degrees but the orientation is always changing.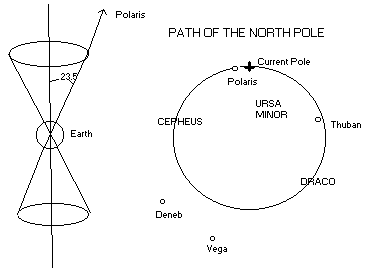

One consequence of precession is that the north star Polaris is drifting. It is only "north star" by coincidence today. Vega will be our north star for a time in the distant future. Another consequence is that precession introduces a difference between a sidereal (real) year and a tropical (by the sun) year because during the course of one year the position of the equinox changes slightly. The physical cause of the precession is a torque (twisting) of the earth, caused mostly by the sun's and the moon's gravity pulling on the equatorial bulges of the earth. If earth were NOT spinning, the sun and moon would pull the earth so that the bulges were flat in the sun-earth orbital plane.

The planets have some gravitational influence also, but insignificant compared to the sun and moon. Still, the planets manage to cause the orbit of earth about the sun to precess and morph. The inclination of Earth's orbit varies with respect to the solar system's invariant plane with a period of roughly 71000 years. Apsidal (Earth's orbit's major axis) precession P = 112,000 yr, combines with the 25,770 yr precession to make it about 21,630 years for the Vernal Equinox to cycle 360 degrees. Planetary perturbations also cause an oscillation in the ellipticity of earth's orbit whose main component 413,000 year long, in which the eccentricity varies from its mean of 0.0019 by +/- 0.012.

Taken in conjunction with the 26000-year spin-axis precession, the 71000-year orbit precession causes a 41000-year oscillation in the tilt of the earths axis, about plus or minus 1.3 degrees from its average value of 23.3 degrees. This number is not absolutely stable - it depends on the combined positions of all the planets through time. The obliquity (tilt) for the last 600,000 years is shown below.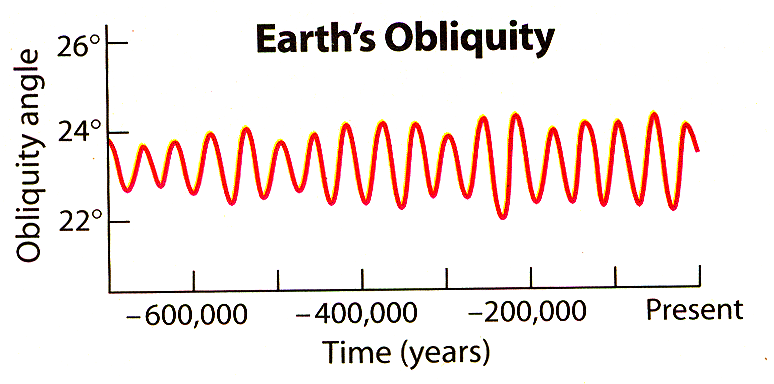

The tilt reached a maximum of 24.2 degrees about 9500 years ago, and has been decreasing ever since. The tilt is now near the average value, but the rate of change of the obliquity is near a maximum.

The most startling consequence of this is that the tropics (the tropics of Cancer and Capricorn, where the most northerly or southerly vertical rays of the sun strike) are moving toward the equator. The rate is more than 14 meters per year! Example: the government of Taiwan erected a monument in a park marking the tropic in 1908. The actual tropic is now more than a kilometer south of this location! The arctic circles are likewise travelling toward their respective poles. The temperate zones gain 1550 square kilometers of territory every year!

Another consequence may be seen in climactic data from oxygen isotope data: there a appears to be a cyclic climate pattern with a 41,000-year period, one of the so-called Milankovitch cycles. This can be qualitatively understood: when the obliquity is low, the polar regions get less sunlight, cool, and accumulate ice and snow. The total amount of sunlight caught by the earth remains the same, so it is premature to positively identify obliquity changes as the root cause of the ice ages." Worthy 2000.